図形を描く系のコードでやっている計算を図解するシリーズ。
Illustratorのスクリプトで円を描くのは次のように簡単です。
// 引数は、(上端、左端、幅、高さ)
activeDocument.activeLayer.pathItems.ellipse(0, 10, 100, 100);
ところが円弧を描こうとするとですね、これが面倒なんですよ。
スクリプトの全体は Gist に置きました。
Illustrator : 2点をつなぐ弧を描く · GitHub
以下でそれぞれの工程について説明します。
主な部分は次のような感じです。

// 点. x, y : float var Point = function(x, y){ this.x = x; this.y = y; } // ------------------------ // o を中心として p1 から反時計回りに p2 へ円弧を描く // p1, p2, o : Point function drawArc(p1, p2, o){ // p1, p2が同じ位置の場合は何もしない if(p1.equals(p2)) return; // 1. 弧の中心角を求める var v1 = p1.sub(o).normalize(); var v2 = p2.sub(o).normalize(); var t = Math.acos(v1.dot(v2)); if(v1.cross(v2) < 0) t = WPI - t; // 2. 始点・終点のハンドルの位置を求める var t1 = p1.getAngle(o); var t2 = p2.getAngle(o); var radius = dist(p1, o); var han = radius * getHandleLengthBase(t); // ハンドル長の決定 // ハンドルの位置 var h1 = new Point().byAngle(t1 + HPI).mul(han).add(p1); var h2 = new Point().byAngle(t2 - HPI).mul(han).add(p2); var p = createAPath().pathPoints; // 3. 中間点のアンカーの位置を決める if(t > Math.PI){ t /= 3; setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p1.rot(t, o), h1.rot(t, o), h2.rot(-t * 2, o)); setPathPoint(p.add(), p2.rot(-t, o), h1.rot(t * 2, o), h2.rot(-t, o)); setPathPoint(p.add(), p2, p2, h2); } else if(t > HPI){ t /= 2; setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p1.rot(t, o), h1.rot(t, o), h2.rot(-t, o)); setPathPoint(p.add(), p2, p2, h2); } else { setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p2, p2, h2); } }
1. 弧の中心角を求める
内積
弧の中心角を求めるために、内積を使っています。
平面上に2つのベクトル ,
があるとき、内積は次のように計算されます。
a.x * b.x + a.y * b.y
// Point のメソッド dot : function(p){ // 内積. p : Point return this.x * p.x + this.y * p.y; },
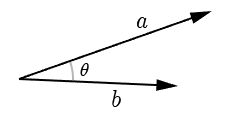
,
のなす角を
とすると、内積(
)と角度には次の関係があります。
( は ベクトル a の長さ(ノルム)を表します。)
,
が単位ベクトルの場合、分母は 1 になるので無視できます。
冒頭のスクリプトではベクトルを正規化(normalize)により単位ベクトルにしているので、
は Math.acos(a.dot(b)) のように求められます。
ただしこの角度は 180度より小さいほうの角度です。
描きたい円弧の中心角が大きい側の場合は修正する必要があります。

外積
角度の修正のために、中心から p1 に視線を向けたとき、p2 は左右どちらにあるかを判定します。

これには外積を使うことができます。
平面上に2つのベクトル ,
があるとき、外積は次のように計算されます。
a.x * b.y - a.y * b.x
// Point のメソッド cross : function(p){ // 外積. p : Point return this.x * p.y - this.y * p.x; },
,
のなす角を
とすると、外積(
)と角度には次の関係があります。
sin の値ですので、 が180~360度の場合はマイナスになります。
外積がマイナスなら、内積から求めた角度 は時計回り方向の角度ということなので、
360度から
を引いて、反時計周り方向の角度に直します。
2. 始点・終点のハンドルの位置を求める
ハンドル長の決定
Illustrator ではベジエ曲線を使うので、曲線を描くときはハンドルの位置を決めないといけません。
一般的に(Illustratorの楕円ツールで描く円くらいの精度で)、半径 1 の円弧を描く場合、
中心角 に対するハンドルの長さは次の式で求められます。
*1
実際に使うハンドルの長さはこれに半径を掛けた値です。
楕円ツールで円を描いた場合、アンカー間の弧の中心角は90度です。
今回の場合、描きたい弧の中心角が90度を超える場合は、 弧の中間にもアンカーを置いてあげないと円弧らしくなりません。
そこで、中心角が90度以下の場合はアンカー2つ、180度以下の場合は3つ、
それより大きい場合は4つで円弧を描くようにしました。
このためアンカー間の弧の中心角は、それぞれ上で求めた中心角の 1/1, ½, 1/3 になり、
これによってハンドルの長さも違ってきます。
以下はこの部分の処理です。
// 弧の中心角に対して半径が1の場合のハンドル長さを返す // t : float, radian function getHandleLengthBase(t){ if(t > Math.PI){ // 4点で描画 t /= 3; } else if(t > HPI){ // 3点で描画 t /= 2; } // else : 2点で描画 return 4 * Math.tan(t / 4) / 3; }
ハンドルの位置を決定
ハンドルの長さが決まったので座標を決めます。
ベジエ曲線の性質として、ハンドルはアンカー位置での接線になります。 また、円の接線は、接点と中心を結んだ線と直角に交わります。
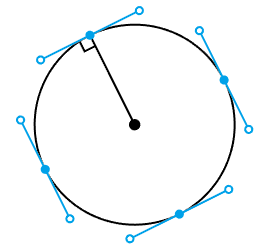
これに基づき、 始点・終点のハンドルの位置は、中心 o から始点・終点を向いたベクトルを それぞれ90度回転させた方向に向けて決めます。
冒頭のサンプルスクリプトでは以下の部分でこれを行っています。
var t1 = p1.getAngle(o); var t2 = p2.getAngle(o); var radius = dist(p1, o); var han = radius * getHandleLengthBase(t); // ハンドル長の決定 // ハンドルの位置 var h1 = new Point().byAngle(t1 + HPI).mul(han).add(p1); var h2 = new Point().byAngle(t2 - HPI).mul(han).add(p2);
3. 中間点のアンカーの位置を決める
円弧の中間に作る点についても、アンカーとハンドルの位置を計算する必要があります。
これらは始点・終点のアンカーとハンドルを、上で求めた角度で回転させれば求められます。
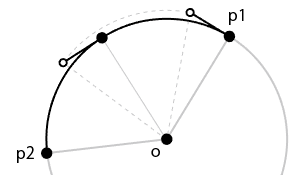
原点を中心に、点 を反時計回りに角度
だけ回転させた座標
は次のようになります。
サンプルスクリプトでは以下のように実装しています。
// Point のメソッド // o を中心に反時計回りに回転する rot : function(t, o){ // t : float (radian), o : Point var c = Math.cos(t); var s = Math.sin(t); var x = this.x - o.x; var y = this.y - o.y; return new Point(x * c - y * s, x * s + y * c).add(o); },
以上です
やろうとしていることに対して非常に面倒な手順ですが、 ベジエ曲線の数式を使わずにできるという意味では、 意外とシンプルな処理とも言えるのではないでしょうか。
*1:Wikipedia英語版 Bézier curve - Wikipedia - #Properties