スクリプトでパステキストを扱う
Illustrator上で入力した文字(テキストオブジェクト)は以下の3種類のいずれかになります。
ポイントテキスト エリアテキスト パステキスト
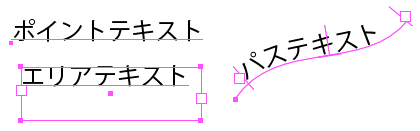
先日、パステキストのパスを初めてJavaScriptで扱ってみたら 色々と発見などがあったので、記事にしたいと思います。
パステキストの判別
JavaScript でテキストオブジェクト(TextFrameItem)の種類を判別するには kind というプロパティを参照します。kind の値は上記の種別と対応した以下の3種類です。
TextType.POINTTEXT TextType.AREATEXT TextType.PATHTEXT
判別の処理は例えば以下のように行います。
// 選択オブジェクトがパステキストのときにメッセージを表示する。 var obj = app.activeDocument.selection[0]; if(obj.typename == "TextFrame" && obj.kind == TextType.PATHTEXT){ // 処理 alert("パステキストです"); }
パス上文字の始点と終点を取得する
パステキストで文字が沿っているパスの情報は、TextFrameItem の textPath というプロパティで取得できます。この値は TextPath オブジェクトです。
また、パス上での文字の始点・終点は、TextFrameItem の startTValue, endTValue から取得できます。
// 選択されているパステキストのstartTValue, endTValueを表示する。 var textFrame = app.activeDocument.selection[0]; alert("startTValue = " + textFrame.startTValue +"\rendTValue = " + textFrame.endTValue);

~TValue( T の値 )という名前から想像できるように、この値はベジエ曲線のパラメーターに基づくものです。 *1
ベジエ曲線のパラメーターは2つのアンカー間の曲線上の位置によって 0~1 の値をとりますが、 ~TValue はこれに始点側アンカーのインデックスを足した値になっています。
例えば、パス上文字の始点がパスの1つ目と2つ目のアンカー の間にある場合、startTValueは 0~1 の間の値になり、 2つ目と3つ目のアンカーの間にある場合は 1~2 の間の値になります。 *2
…というのはオープンパスの場合で、 クローズパスの場合はもう少し考慮が必要な点があります。
クローズパスの場合
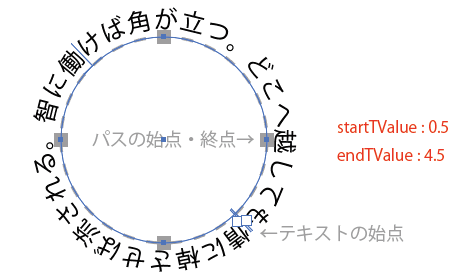
まず、上の図ではパスのアンカーは4つなので、 上記の考え方からすると startTValue と endTValue は 0~4 の間の値になりそうなんですが、 ここでの endTValue は 4.5 という値になっています。
文字がパスの始点(=終点)をまたいでいるので、 こうなるのだろうなという感じではありますが、 さらにこの文字の始点・終点を手作業で動かすと、 下の画像のようなおかしな値になります。
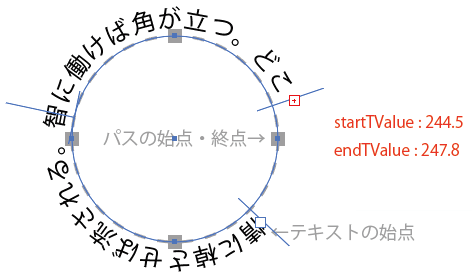
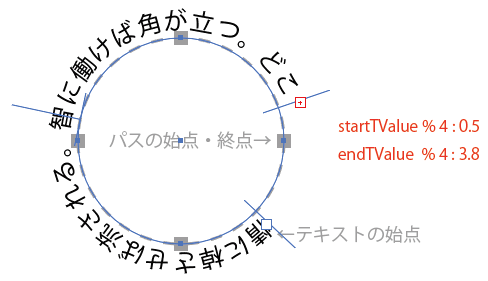
内部でどういう計算をしているのかわかりませんが、 この値から最初の画像のような素直な値を 取得するには、アンカーの数で割った余りを取得すればよいようです。 (次項の「注意が必要な点」も考慮してください。)
パス上文字の始点と終点を設定する
startTValue, endTValue は、適当な値を代入することで変更できます。
startTValue に 0、 endTValue に「アンカー数マイナス1」を設定すると、 パス上文字の範囲がパスの始点と終点になります。
注意が必要な点は、endTValue に startTValue より小さい値を設定するとエラー になることです。
前項のクローズパスでの性質を考慮して パステキスト (クローズパス)に startTValue, endTValue を設定する処理を function にすると以下のように書くことができます。
function setTValue(textFrame, startT, endT){ var len = textFrame.textPath.pathPoints.length; startT %= len; endT %= len; if(endT < startT){ endT += len; } textFrame.startTValue = startT; textFrame.endTValue = endT; }
スクリプトによるパステキストのパスの変更
TextPath は通常のパスと同じように pathPoints などの属性を持っているため、 スクリプトでアンカーやハンドルの位置や数を変えることができます。 (PathItem とはプロパティやメソッドが異なる部分もあります。)
スクリプトで TextPath の pathPoints を操作する場合に注意が必要な点は、 startTValue, endTValue の値が変わってくれないことです。 このため、処理によってアンカー数が変わる場合は、 これらの値の変更も必要になることがあります。
別に掲載 している「 円弧にする 」というスクリプトの中にこの位置の調整処理があります。 このスクリプトには下の画像のようにパステキストが沿うパスを 適当な円弧にする機能がありますが、 TextPath のアンカー数を変更し、パスの長さも変わるので、 文字の位置を再設定する必要があるのです。

処理はベジエ曲線に関する汎用的な操作(計算)の組み合わせです。 詳しくはここで書くと長くなるので、追って記事を作ろうと思いますが、 工程だけ順を追って書くと以下のようなことをしています。
1. パスの長さ ( L1 ) を算出する。 2. パスの始点から startTValue にあたるパス上の点までの長さ ( S1 ) を算出する。 3. L1 に対する S1 の割合 ( R ) を算出する。 4. パスを変更する。 5. 変更後のパスの長さ ( L2 ) を算出する。 6. L2 に割合 R を掛けた長さ ( S2 ) を算出する。 7. パスの始点からの長さが S2 になるパス上の点のパラメーターを算出する。 パラメーターとアンカーのインデックスから startTValue が求められる。 8. startTValue を設定する。 (endTValue についても同様に行う。)
パスの長さを計算しているのは、TextPath に length というプロパティがないためです。
undoの問題
スクリプトで startTValue, endTValue を変更した場合、 スクリプト実行後に undo をしてもこれらが実行前の値に戻らないようです。
スクリプトでの変更は undo の対象になっていないのか、 内部的な仕組みはよくわかりませんが、
これについては今のところ以下のような手順で処理をして回避しています。
1. 元のパスを複製 2. 複製したパスを操作 3. 元のパスを削除
こうすると undo はパス自体の変更ではなく削除の undo になるので、 文字の位置は実行前の状態に戻ります。
文字を添わせる側を操作する
パステキストは手作業での操作により文字をパスの反対側に添わせることができますが、 このとき TextPath の polarity というプロパティの値が PolarityValues.NEGATIVE になります。 polarity の既定値は PolarityValues.POSITIVE です。
polarity はスクリプトで設定することもできます。
// パステキスト(文字は既定の側に沿う)を選択して実行すると、 // 文字がパスの反対側に沿う。 var textFrame = app.activeDocument.selection[0]; textFrame.textPath.polarity = PolarityValues.NEGATIVE;

polarity が NEGATIVE になると、パスの向き(PathPoint の順番)が逆になります。 このとき、startTValue と endTValue は元のパスの終点を 0 とした値となります。
とりあえず以上です
。
反転変換(円に関する反転)について(3)

上の図は、真ん中の「1」を囲んでいる四角形のような形を、 四つの辺(円弧)に関してそれぞれ反転して「2」の位置に移し、 さらにそれを「3」・「4」の位置に反転して移し、… という手順で描かれています。
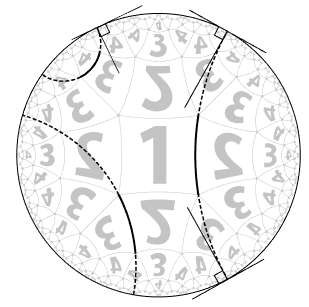
このような図を描くために必要な決まりごとは、 これらの辺に使われている円弧を、 外側の円周と垂直に交わる円の一部とすることです。 *1
双曲幾何学のモデルの1つであるポアンカレ円板では このような円弧が「直線」という扱いになります。(以下、双曲直線という。)
ネットを hyperbolic tessellation, hyperbolic tiling などで画像検索すると似たような感じの図がいろいろ出てきます。
円板の中に表されている双曲平面とは何か?ということから 調べていくと気が遠くなってくるのですが、
とりあえず上のような図を描くために必要なのは、 この双曲直線、要するに円弧を作図する方法です。
双曲直線を作図する

円の内部の2点を通る双曲直線は、片方の点を円に関して反転し、 これらの3点を通る円を作図することで描けます。

また、2点を通る双曲直線に関して別の1点を反転させる場合は、 まず2点を通る双曲直線を取得し、それに関して別の1点を反転変換するという 処理になります。
Illustrator用のサンプルスクリプトを Gist に置きました。
Illustrator:ポアンカレ円板上での反転関連 · GitHub
内部処理に関しては以下の過去記事で書いています。
反転 →「
反転変換(円に関する反転)について(1) - s.h's page
」
2点をつなぐ円弧 →「
2点をつなぐ弧を描く - s.h's page
」
最初の図も、このスクリプトを使って点を1つずつ反転しては 円弧でつないで、という地道な作業によって作ったのですよ。 *2
もっと複雑なのを描こうと思ったら スクリプトで全部やらせる方向になるでしょう。
参考文献
上の双曲直線の作図方法は「作図で身につく双曲幾何学」(阿原一志 著、共立出版 2016)
という本に掲載されていたものです。
ネットで双曲幾何学について調べていていまいち要領を得なかったのですが、
この本では作図から入るので感覚的にわかりやすかったです。
(※ 基本を抑える感じの内容なので、冒頭の図のようなものの作図は扱われていません。)
作図で身につく双曲幾何学: GeoGebraで見る非ユークリッドな世界 | 阿原 一志 |本 | 通販 | Amazon
2点をつなぐ弧を描く
図形を描く系のコードでやっている計算を図解するシリーズ。
Illustratorのスクリプトで円を描くのは次のように簡単です。
// 引数は、(上端、左端、幅、高さ)
activeDocument.activeLayer.pathItems.ellipse(0, 10, 100, 100);
ところが円弧を描こうとするとですね、これが面倒なんですよ。
スクリプトの全体は Gist に置きました。
Illustrator : 2点をつなぐ弧を描く · GitHub
以下でそれぞれの工程について説明します。
主な部分は次のような感じです。

// 点. x, y : float var Point = function(x, y){ this.x = x; this.y = y; } // ------------------------ // o を中心として p1 から反時計回りに p2 へ円弧を描く // p1, p2, o : Point function drawArc(p1, p2, o){ // p1, p2が同じ位置の場合は何もしない if(p1.equals(p2)) return; // 1. 弧の中心角を求める var v1 = p1.sub(o).normalize(); var v2 = p2.sub(o).normalize(); var t = Math.acos(v1.dot(v2)); if(v1.cross(v2) < 0) t = WPI - t; // 2. 始点・終点のハンドルの位置を求める var t1 = p1.getAngle(o); var t2 = p2.getAngle(o); var radius = dist(p1, o); var han = radius * getHandleLengthBase(t); // ハンドル長の決定 // ハンドルの位置 var h1 = new Point().byAngle(t1 + HPI).mul(han).add(p1); var h2 = new Point().byAngle(t2 - HPI).mul(han).add(p2); var p = createAPath().pathPoints; // 3. 中間点のアンカーの位置を決める if(t > Math.PI){ t /= 3; setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p1.rot(t, o), h1.rot(t, o), h2.rot(-t * 2, o)); setPathPoint(p.add(), p2.rot(-t, o), h1.rot(t * 2, o), h2.rot(-t, o)); setPathPoint(p.add(), p2, p2, h2); } else if(t > HPI){ t /= 2; setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p1.rot(t, o), h1.rot(t, o), h2.rot(-t, o)); setPathPoint(p.add(), p2, p2, h2); } else { setPathPoint(p.add(), p1, h1, p1); setPathPoint(p.add(), p2, p2, h2); } }
1. 弧の中心角を求める
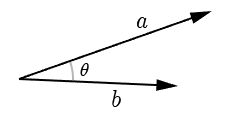
内積
弧の中心角を求めるために、内積を使っています。
平面上に2つのベクトル ,
があるとき、内積は次のように計算されます。
a.x * b.x + a.y * b.y
// Point のメソッド dot : function(p){ // 内積. p : Point return this.x * p.x + this.y * p.y; },
,
のなす角を
とすると、内積(
)と角度には次の関係があります。
( は ベクトル a の長さ(ノルム)を表します。)
,
が単位ベクトルの場合、分母は 1 になるので無視できます。
冒頭のスクリプトではベクトルを正規化(normalize)により単位ベクトルにしているので、
は Math.acos(a.dot(b)) のように求められます。
ただしこの角度は 180度より小さいほうの角度です。
描きたい円弧の中心角が大きい側の場合は修正する必要があります。

外積
角度の修正のために、中心から p1 に視線を向けたとき、p2 は左右どちらにあるかを判定します。

これには外積を使うことができます。
平面上に2つのベクトル ,
があるとき、外積は次のように計算されます。
a.x * b.y - a.y * b.x
// Point のメソッド cross : function(p){ // 外積. p : Point return this.x * p.y - this.y * p.x; },
,
のなす角を
とすると、外積(
)と角度には次の関係があります。
sin の値ですので、 が180~360度の場合はマイナスになります。
外積がマイナスなら、内積から求めた角度 は時計回り方向の角度ということなので、
360度から
を引いて、反時計周り方向の角度に直します。
2. 始点・終点のハンドルの位置を求める
ハンドル長の決定
Illustrator ではベジエ曲線を使うので、曲線を描くときはハンドルの位置を決めないといけません。
一般的に(Illustratorの楕円ツールで描く円くらいの精度で)、半径 1 の円弧を描く場合、
中心角 に対するハンドルの長さは次の式で求められます。
*1
実際に使うハンドルの長さはこれに半径を掛けた値です。
楕円ツールで円を描いた場合、アンカー間の弧の中心角は90度です。
今回の場合、描きたい弧の中心角が90度を超える場合は、 弧の中間にもアンカーを置いてあげないと円弧らしくなりません。
そこで、中心角が90度以下の場合はアンカー2つ、180度以下の場合は3つ、
それより大きい場合は4つで円弧を描くようにしました。
このためアンカー間の弧の中心角は、それぞれ上で求めた中心角の 1/1, ½, 1/3 になり、
これによってハンドルの長さも違ってきます。
以下はこの部分の処理です。
// 弧の中心角に対して半径が1の場合のハンドル長さを返す // t : float, radian function getHandleLengthBase(t){ if(t > Math.PI){ // 4点で描画 t /= 3; } else if(t > HPI){ // 3点で描画 t /= 2; } // else : 2点で描画 return 4 * Math.tan(t / 4) / 3; }
ハンドルの位置を決定
ハンドルの長さが決まったので座標を決めます。
ベジエ曲線の性質として、ハンドルはアンカー位置での接線になります。 また、円の接線は、接点と中心を結んだ線と直角に交わります。
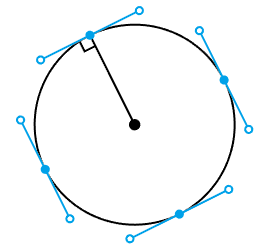
これに基づき、 始点・終点のハンドルの位置は、中心 o から始点・終点を向いたベクトルを それぞれ90度回転させた方向に向けて決めます。
冒頭のサンプルスクリプトでは以下の部分でこれを行っています。
var t1 = p1.getAngle(o); var t2 = p2.getAngle(o); var radius = dist(p1, o); var han = radius * getHandleLengthBase(t); // ハンドル長の決定 // ハンドルの位置 var h1 = new Point().byAngle(t1 + HPI).mul(han).add(p1); var h2 = new Point().byAngle(t2 - HPI).mul(han).add(p2);
3. 中間点のアンカーの位置を決める
円弧の中間に作る点についても、アンカーとハンドルの位置を計算する必要があります。
これらは始点・終点のアンカーとハンドルを、上で求めた角度で回転させれば求められます。
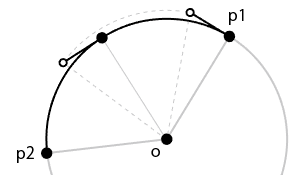
原点を中心に、点 を反時計回りに角度
だけ回転させた座標
は次のようになります。
サンプルスクリプトでは以下のように実装しています。
// Point のメソッド // o を中心に反時計回りに回転する rot : function(t, o){ // t : float (radian), o : Point var c = Math.cos(t); var s = Math.sin(t); var x = this.x - o.x; var y = this.y - o.y; return new Point(x * c - y * s, x * s + y * c).add(o); },
以上です
やろうとしていることに対して非常に面倒な手順ですが、 ベジエ曲線の数式を使わずにできるという意味では、 意外とシンプルな処理とも言えるのではないでしょうか。
*1:Wikipedia英語版 Bézier curve - Wikipedia - #Properties
